Mis soluciones al examen de Dibujo Técnico II de la Junta de Andalucía, convocatoria ordinaria suplente del año 2024

    Comento mis soluciones a los ejercicios del examen de Dibujo Técnico II de la convocatoria ordinaria suplente de este año 2024. Estos enunciados están publicados en la página web de la Universidad de Andalucía en la sección de exámenes de PEvAU o antigua selectividad.

    Procedo a distribuirlos por los bloques I y II y sus correspondientes apartados (problemas y ejercicios)

BLOQUE I

PROBLEMA 1: SISTEMA DIÉDRICO

    Nos dan las proyecciones de dos puntos y tenemos que pasar por ellos un plano que forma 45º con el plano horizontal de proyección. De todas las opciones que podemos dibujar, nos piden que dibujemos las trazas que formen un ángulo agudo en el primer diedro o cuadrante. En la imagen es el plano P en color verde.

    Los puntos dato, A y B, son los vértices consecutivos de un tetraedro que tenemos que dibujar apoyado sobre el plano P. He abatido el plano para colocar la base y he aprovechado en el abatimiento para poder calcular la altura de dicho poliedro regular. Colores magenta y azul.

    Por último, he indicado las partes vistas y ocultas del sólido y la altura numérica del poliedro, como se perdía en el enunciado.

PROBLEMA 2: SISTEMA AXONOMÉTRICO

    Dadas las vistas de un sólido: planta, alzado y perfil derecho a escala 2:3; nos piden dibujar la perspectiva isométrica de la pieza a escala natural 1:1. También quieren que indiquemos la medida real de la magnitud "C".

    Como las vistas están a una escala y tenemos que incluir el coeficiente de reducción, he indicado los pasos numéricos que tenemos que seguir para poder realizar las operaciones con un solo cálculo. En color verde.

    El valor numérico de "C" se calcula aplicando la escala 2:3.

BLOQUE II

EJERCICIO 1: TRAZADOS GEOMÉTRICOS

    Nos dan dos circunferencias y el punto de tangencia en una de ellas. Nos piden el eje radical de las dos circunferencias dadas y las circunferencias tangentes a ambas, cuyo punto de tangencia sea T.

    He hallado el eje radical de ambas circunferencias, en color verde. Y he aplicado los procedimientos de Apolonio para resolver este caso que es un caso especial de CCT (circunferencia, circunferencia, punto).

EJERCICIO 2: TRANSFORMACIONES GEOMÉTRICAS

    Nos encontramos una homología afín determinada por tres puntos afines, A-A', O-O' y N-N', este último es un punto doble. Nos piden que hallemos la figura afín a la dada (parece un lapicero) y dibujar el eje de la afinidad, así como, los semiejes de la elipse. 

    He hallado los semiejes de la mitad de la elipse en la que se transforma la mitad de la circunferencia que se nos representa como una goma del lápiz.  En color magenta.

    El resto de la figura se resuelve como una afinidad normal. He aprovechado el paralelismo entre las rectas y el paralelismo que tienen algunos segmentos con el eje. Recordar que la afinidad mantiene el paralelismo entre rectas.

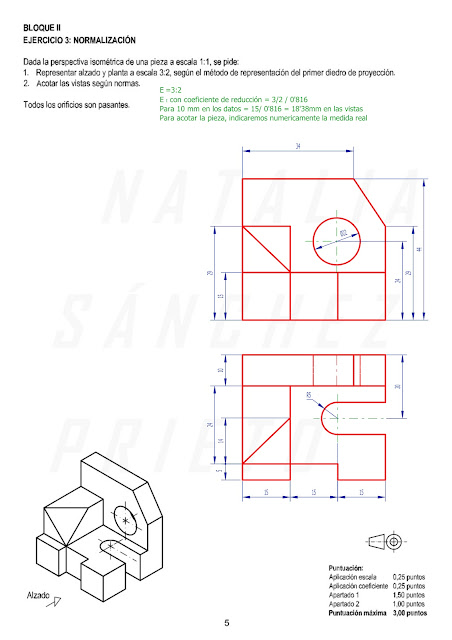
EJERCICIO 3: NORMALIZACIÓN

    Tenemos dibujado una perspectiva isométrica a escala natural 1:1, y nos piden dibujar la planta y el alzado a escala 3:2 para luego acotarla según normas.

    Las operaciones oportunas que tenemos que realizar con las escalas las he puesto en color verde. 

    La acotación obedece a las medidas reales, las he calculado a partir de las vistas y aplicando la escala.

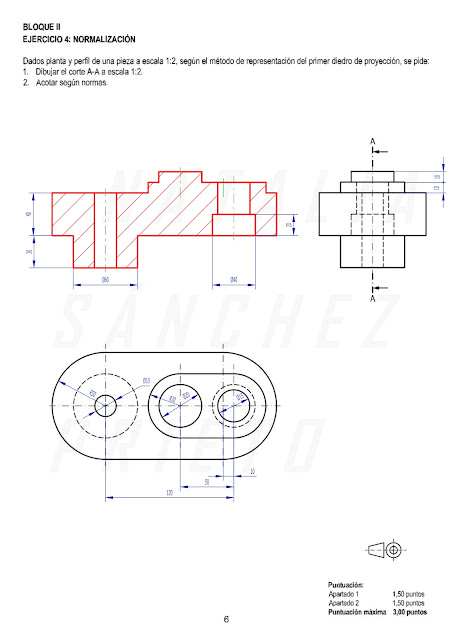
EJERCICIO 4: NORMALIZACIÓN

    Tenemos que realizar el corte A-A en alzado de la pieza dada por su planta y perfil izquierdo. Las vistas están dibujadas a escala 1:2.

    He realizado el corte y acotado poniendo las medias reales que se deducen de aplicar la escala 1:2. Lo más reseñable de esta pieza, a mi parecer, es la colocación de las circunferencias y su acotación.

    Estos son mis comentarios a mis soluciones al examen suplente de Dibujo Técnico II de la PEvAU de Andalucía del año 2024.

EvAU Comunidad de Madrid mi solución examen extraordinario coincidentes Dibujo Técnico 2024

     Vamos por el último post de la EvAU (antigua selectividad y PAU) de la Comunidad de Madrid del examen de Dibujo Técnico II del año 2024 de la convocatoria extraordinaria y coincidentes (de los exámenes de las asignaturas específicas) de Julio. Quiero recordar que la intención de mis post es intentar ser aclaratorios, complementarios a cualquier publicación haya realizado cualquier universidad madrileña con las soluciones a dicho examen. 

    Procedo a distribuir los problemas planteados por opciones, bloques y ejercicios

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO A1.

    En el ejercicio aparecían dibujados dos rectas y un punto. Nos pedía determinar las circunferencias tangentes a las rectas y que a su vez pasaran por el punto dado A.

    Lo he resuelto por potencia, como nos indica Apolonio en el caso de punto recta recta (rrP). 

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO A2

    Nos dan tres rectas: h, s y r. Nos piden dibujar la recta paralela a h que se apoya o corta a r y s. 

    Lo he resuelto por cambio de plano. He dibujado dos planos paralelos a h que contuvieran a r y a s. Después, he hallado la intersección de ambos planos. La recta intersección de estos planos es la solución pedida, la recta m.

    Otra manera de resolverlo hubiera sido hallando un plano paralelo a h que pasara por una de las rectas, r o s. Y después, hallar la intersección de este plano con la otra recta. Por último, trazamos la paralela a h por ese punto de intersección.

    Viene comprobado en color magenta que la recta m efectivamente corta a r y s en un punto.

• SISTEMA AXONOMÉTRICO. EJERCICIO A3.

    Venían dibujadas la planta y el alzado de una pieza. Nos pedían que representar la pieza el dibujo isométrico (sin coeficiente de reducción). Las circunferencias isométricas las debíamos dibujar cómo óvalo isométrico y no como elipses. También teníamos que indicar los centros de las circunferencias que definen dichos óvalos.

    He dibujado las partes útiles del cuadrado que circunscribe la circunferencia para poder indicar y calcular dichos los centros.

    Después, los he desplazado siguiendo el eje z y el eje y, para obtener el grosor de la figura.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO A4

    Tenemos una pieza representada en dibujo isométrico (sin coeficiente de reducción) y nos piden que realicemos las vistas necesarias con las secciones que consideremos oportunas para poder definir la pieza. También pedían acotar las vistas para su definición dimensional siguiendo las normas ISO y UNE.

    El alzado y la planta son vistas suficientes para poder apreciar el volumen de la pieza. Y para poder acotar la parte interna izquierda, la cota 10, he optado por un corte parcial.

    En la acotación, donde más variaciones de cotas podemos encontrar es en la parte derecha de la pieza. Hemos indicado las totalidades y los radios.

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO B1.

    Nos dan dos puntos de una parábola y su foco. Teníamos que hallar la directriz, el eje y las tangentes por esos puntos a la parábola.

    Hemos dibujado las circunferencias que pasan por F y tienen sus centros en A y B. La directriz será la tangente exterior a dichas circunferencias, he escogido la tangente superior. Perpendicular a la directriz por el foco se encuentra el eje.

    Para trazar las tangentes, hemos dibujado los radios vectores, y perpendicular a la línea que une los extremos, estarán las tangentes.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO B2

    Tenemos que hallar la sección que produce el plano ABCD en el paralepípedo o ortoedro. 

    Como el plano ABCD es un plano paralelo a la línea de tierra, he resuelto la sección en tercera proyección. 

    También he incluido los lados vistos y ocultos de la figura plana sección.

• PERSPECTIVA CÓNICA. EJERCICIO B3

    Sobre un poliedro en perspectiva cónica, debemos dibujar la pieza que viene dada por sus tres vistas: planta, alzado y perfil.

    El misterio de este ejercicio se encontraba en hallar el punto medio del alzado. Para poder hallarlo, he obtenido el punto de fuga de las aristas paralelas y dibujado las diagonales de la planta. En color verde. 

    Para concretar la pieza he unido convenientemente los puntos obtenidos en las aristas del sólido.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO B4

    Tenemos en dibujo isométrico (sin coeficiente de reducción), una pieza cuyo plano de simetría horizontal era coincidente con el plano xoy. Había que dibujar las vistas necesarias para poder acotar la pieza con los cortes necesarios para su correcta definición. Hay que tener en cuenta las normas industriales ISO y UNE para su ejecución.

    En el alzado le hemos aplicado un corte al cuarto. En las medidas hemos tenido el cuenta el plano de simetría que definen el eje y. 

    Esta es mi propuesta a la solución al examen de EvAU de la convocatoria extraordinaria coincidentes del año 2024 de la Comunidad de Madrid de Dibujo Técnico II.

EvAU Comunidad de Madrid mi solución examen extraordinario Dibujo Técnico 2024

     Voy a exponer mi propuesta a las soluciones al examen de Dibujo Técnico II de la EvAU (antigua selectividad o PAU) de la Comunidad de Madrid de la convocatoria extraordinaria que se celebró en Julio de 2024. Recordar que la Universidad Complutense de Madrid (supongo que otras Universidades madrileñas también las compartirán) comparte las soluciones, y yo trato de aportar, cuando se pueda, una alternativa o un complemento a estas soluciones.

    Procedo a distribuir el examen por bloques y ejercicios.

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO A1.

    Nos dan una figura, ABCD, formada por un arco y tres rectas. Tenemos que transformarla en una figura inversa. Los datos de la inversión son el centro y un punto doble.

    Tenemos los dos casos importantes de la transformación de una recta: la que pasa por O que se transforma en sí misma, y la que no pasa por O que se transforma en una circunferencia que si pasa por O. Sabemos que O es el centro de inversión y que E un punto doble. Dibujamos la circunferencia de puntos dobles y con ella podemos calculamos los inversos de A y D que son A' y D', respectivamente. Después, aplicamos los casos indicados al inicio del párrafo.

    Con los arcos que pasan por A' y D' hallamos B' y C', y con ello la recta inversa que resulta de transformar el arco de BC.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO A2

    Nos dan una semiesfera y la proyección horizontal de un punto A. Nos dicen que A es el punto perteneciente a la semiesfera y que por A pasa una recta frontal que atraviesa el sólido. El punto B, es el punto de salida de la recta frontal y además se encuentra situado a una distancia d de A.
    Para resolverlo, he pasado un plano frontal por el punto A. He hallado la sección de ese plano frontal con la semiesfera para poder calcular la posición de los puntos A y B.
    Por último, he diferenciado las partes vistas de las ocultas de la recta.

• PERSPECTIVA CÓNICA. EJERCICIO A3

    En este ejercicio, proponen que dibujemos la sección que produce un plano que pasa por tres puntos A, B y C en un poliedro. 
    Como es una perspectiva cónica frontal, sabemos que las rectas paralelas al plano geometral se van a seguir viendo paralelas en cualquier otra altura o posición. He consderado el sólido como si fuera un paralepípedo. El segmento AB se encuentra en la cara superior, paralela al suelo, por lo tanto, si cortamos el sólido por un plano horizontal que pasa por C, la sección que produce será un paralelogramo igual que sus bases, en color azul claro. Al trazar la paralela por C a AB donde corte, en este caso, con la arista opuesta, tendremos un punto de la sección.
    La sección azul clara es la que se produciría si el sólido fuera un paralepípedo. Para dibujar la solución tomaremos los puntos en común las aristas del poliedro con la sección azul, en color rojo. 

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO A4
    Dada la perspectiva isométrica de una pieza, nos piden representar las tres vistas: planta, alzado y perfil derecho.
    Al ser un dibujo isométrico no tenemos que tener en cuenta el coeficiente de reducción (0'816:1), tomaremos las medidas directamente, siempre que estén sobre aristas paralelas a los ejes coordenados.

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO B1.

    En este ejercicio nos dan una figura ABCDE y tenemos que hallar su figura afín A'B'C'D'E'. Para definir la homología afín, aparecen dibujados el eje y dos puntos afines, A y A'.

    He empezado a dibujar la recta AB, por pasar por A y ser paralela al eje. Las rectas paralelas al eje sus afines también serán paralelas entre sí, por ser su punto doble impropio. Después he hallado B' trazando paralela a la dirección de afinidad.

    Lo siguiente que podemos hacer es hallar las afines de las rectas AE o BC, usando el corte del las prolongación de las mismas con el eje, es decir, su punto doble. De esta manera podemos ir acabando la figura afín.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. B2

    Como datos tenemos dibujados dos rectas h y r y un punto P. Nos piden que dibujemos una recta perpendicular a ambas y que pase por P.
    Mi proceder ha sido: hallar el plano que contiene a P y es paralelo a  h y r  y después trazar la recta perpendicular a dicho plano. Para hallar la dirección de la recta perpendicular al plano, he usado las rectas frontales y horizontales de dicho plano.

• PLANOS ACOTADOS. EJERCICIO B3

    Nos dan el contorno exterior de una cubierta, cuyas vertientes tienen una inclinación de 30º con el plano horizontal de proyección. Al no indicar nada en el enunciado, entendemos que los faldones se encuentra a la misma altura. Nos piden dibujar la parte que falta del tejado.
    Al tener todos los faldones la misma inclinación, he trazado la bisectriz para aquellos que sus trazas forman un ángulo, en este caso de 90º. Para los tejados cuyas trazas son paralelas, hemos trazado la mediatriz. 
    Para la zona interior, hemos prolongado las trazas hasta que se corten y hemos trazado su bisectriz.
    Marcando convenientemente estas líneas, obtenemos las aristas de intersección que produce estos planos de 30º, es decir, las limatesas, limahoyas y caballetes.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO B4

    Partimos de la planta y la mitad del alzado cortado a un cuarto, en concreto la parte afectada por el corte (la parte interna). Nos piden: hallar la parte externa del alzado que falta y acotarlo.
    He dibujado la parte externa que falta del alzado y acotado la pieza. Destacar que la planta se ha usado la acotación por simetría y en el alzado se han indicado los radios de la parte superior, son así por ser arcos de 180º. 

    Esta es mi propuesta de solución al examen de Dibujo Técnico II de la EvAU de la Comunidad de Madrid en su convocatoria extraordinaria del año 2024.

Mis soluciones al examen de Dibujo Técnico II de la Junta de Andalucía, convocatoria ordinaria titular del año 2024

     Comparto mis soluciones a examen de la antigua selectividad o PAU o actual PEvAU del distrito único de la Junta de Andalucía. En concreto, el examen titular de Dibujo Técnico de la convocatoria ordinaria del año 2024.

    Comento los problemas y ejercicios por bloques y orden de aparición en el examen.

BLOQUE I

PROBLEMA 1: SISTEMA DIÉDRICO

    Teníamos que dibujar una esfera de centro O, tangente al plano proyectante P. El punto de tangencia T es inmediato por ser plano P  proyectante. Este punto T estaba en la recta perpendicular al plano que pasa por O, OT es el radio de la esfera. En color Verde.

    Después había que hallar la sección que producía a la esfera un plano Q paralelo a P ya una distancia de 50 mm de P. Trazamos el plano, la sección,  y la verdadera magnitud a través de un abatimiento. En color magenta.

    Con la recta R, teníamos que hallar los puntos de intersección con la esfera y la visibilidad. Y por último, la distancia del punto T a la recta R. En color naranja.

    Y como siempre las soluciones en color rojo y los datos en negro.

PROBLEMA 2: SISTEMA AXONOMÉTRICO

    Nos daban las tres vistas de un sólido;:planta, alzado y perfil,  a escala 6:5, según el sistema europeo o del primer diedro de proyección.

    Teníamos que dibujar la perspectiva isométrica de la pieza a escala 5:2. Se ha indicado en verde los cálculos oportunos para poder hacer el cambio de escala e introducir el coeficiente de reducción. 

    Para hallar la media real de C, hemos aplicado la escala 6:5.

BLOQUE II

EJERCICIO 1: TRAZADOS GEOMÉTRICOS

    Nos dan dos rectas y un punto, tenemos que trazar las circunferencias tangentes a ambas rectas que pasen por el punto.

    Lo hemos resuelto por los casos de Apolonio, el caso recta recta punto RRP, usando los conceptos de Potencia, Eje Radical y Centro Radical.

EJERCICIO 2: TRANSFORMACIONES GEOMÉTRICAS

    Definiendo una homología afín por su eje y dos puntos afines, nos piden dibujar la figura afín dada formada por dos circunferencias concéntricas y un triángulo. Parece una flecha redonda.

    Era necesario hallar los ejes de las curvas cónicas homólogas de las circunferencias, es decir, los ejes de las elipses afines a las circunferencias dadas. Por que nos lo pedían en el enunciado.

    Una vez halladas las elipses, hemos dibujado el triángulo homólogo, es decir, lo que parece una punta de flecha.

EJERCICIO 3: NORMALIZACIÓN

    Partiendo de un perspectiva isométrica de una pieza a escala 3:2, teníamos que dibujar la planta y el alzado a escala 8:5.

    Para poder dibujar las vistas, hemos explicado en verde cómo pasar de una escala a otra e incluir el coeficiente de reducción en una sóla operación, viene escrito en color verde.

    Las cotas, cómo van en medidas reales, hemos utilizado la escala de las vistas, 8:5. También podríamos haber deducido las medidas de la perspectiva, usando la escala 3:2 e incluyendo el coeficiente de reducción. 

    El sistema de acotación principalmente usado es de simetría.

EJERCICIO 4: NORMALIZACIÓN

    Dada la planta y el perfil de una pieza a escala 1:2, nos pedían realizar el alzado cortado por el plano A-A, y acotar las vistas.

    Se ha realizado el corte y la acotación. Las medidas responden a la verdadera magnitud, es decir, medidas las medidas se indicarán al doble. 

    En cuanto la acotación, indicaremos que hemos puesto el símbolo de cuadrado para poder omitir dos cotas iguales. Podemos ver en planta que prima la simetría y la distribución de las circunferencias de la pieza.

    Hasta aquí mi propuesta de solución al examen de Dibujo Técnico II de la PEvAU de Junio del 2024.

EvAU Comunidad de Madrid mi solución examen ordinario coincidentes Dibujo Técnico 2024

     Nos faltaba por compartir la pareja del examen de la EvAU, ya sabemos antigua selectividad o PAU, de la Comunidad de Madrid de Dibujo Técnico II de la convocatoria ordinaria del año 2024, pero, en este caso es el examen para los futuros alumnos universitarios cuyo examen le coincidían con otra asignatura específica. El denominado "coincidentes". 

    Como hemos hecho en ocasiones anteriores vamos a dividir los ejercicios por bloques que se definen currículo oficial de la asignatura de Dibujo Técnico y por opciones A y B.

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. A1

    Nos dan dibujados un centro de inversión y un rectángulo ABCD. Nos piden hallar la figura inversa de ese rectángulo sabiendo que A y B son puntos dobles.

    Podemos hallar la circunferencia de puntos dobles porque sabemos que A y B son puntos dobles y que su centro está en el centro de inversión. Resulta que el centro de inversión se encuentra en el centro del polígono, por lo tanto la cpd (circunferencia de puntos dobles) pasará por lo vértices del rectángulo, convirtiéndolos también en puntos dobles. Es decir, C y D son C' y D respectivamente.

    Para realizar la figura inversa aplicaremos el teorema de: que una recta que no pasa por el centro de inversión se transforma en una circunferencia que sí pasa por el centro de inversión.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN

• SISTEMA DIÉDRICO. A2

    Tenemos que hallar las proyecciones de un triángulo equilátero situado en el plano que definen el punto A y la recta r. Sabiendo un lado del triángulo AB: el vértice A y la proyección vertical  del vértice B.

    Resulta que la recta r es una recta vertical contenida en el plano vertical de proyección. Por lo tanto, será la traza vertical del plano y por lo tanto un plano proyectante horizontal o también denominado plano vertical.

    Abatimos el plano para poder dibujar la verdadera magnitud del triángulo equilátero y sus proyecciones horizontal y vertical. 

• PERSPECTIVA CABALLERA Y VISTAS. A3

    Este ejercicio consiste en hallar el dibujo isométrico de una pieza dada por sus tres vistas diédricas: planta, alzado y perfil derecho. Se pide omitir las aristas ocultas.

    Recordar que al pedir dibujo isométrico no tenemos que aplicar el coeficiente de reducción isométrico, que es 0'816:1.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. A4

    Tenemos dibujados la "planta" y el "perfil izquierdo" cortada "a un cuarto" de una pieza, se pide: dibujar la parte que falta al aplicarle el "corte al cuarto" en el perfil y el alzado con otro "corte al cuarto". Para acabar el ejercicio tenemos que acotar la pieza para su correcta definición dimensional empleando las normas UNe e ISO. 

    Comentar, que el el perfil hemos girado uno de los agujeros de la base para que se pueda definir como agujero pasante, debido a que es la manera de poder verlo como tal. Y la otra razón es que nos dan dibujados los ejes girados.

     Por lo demás se ha realizado la acotación: por simetría en la parte superior, por elementos iguales en la parte inferior  y el resto de la pieza como una pieza de revolución. No se han colocado los ejes en la parte inferior de la planta por claridad el dibujo.

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. B1

    En este ejercicio nos piden dibujar la figura homóloga de la dada ABC, sabiendo el eje, el centro y la recta límite de la figura no prima de dicha homología.

    Empezamos hallando la recta homóloga de la recta AB, compuesta por los puntos 1ABM. Esta recta pasará por el punto M' y es paralela a la recta O1. Para hallar los puntos A' y B', trazamos los rayos de homología que pasan por los puntos A y B.

    Después hemos dibujado la homóloga de la BCN, la recta B'C'N'. Y realizado el mismo procedimiento anterior para hallar B' y C'.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN

• SISTEMA DIÉDRICO. B2

    Nos piden dibujar los ejes de la elipse sección que produce el plano ABCD en el cono dado y su la verdadera magnitud.

    Para hallar los ejes, hemos trazado la recta frontal que pasa por E y F. Esta recta frontal se encuentra en el plano de simetría del cono que es paralelo al plano vertical de proyección. El otro eje se encontrará en la recta de punta que pasa por el punto medio del eje EF, el punto O. 

    Calculamos la magnitud del semieje menor con la cuerda de la circunferencia sección del plano paralelo a la base que pasa por O.

• PERSPECTIVA CÓNICA. B3

    Nos piden hallar la sección que produce el plano que pasa por tres puntos, ABC, en el sólido. 

    Sabemos que es una perspectiva cónica frontal, las aristas de las caras frontales son paralelos entre sí. 

    Dibujamos el triángulo ABC en perspectiva directa y su proyección sobre el plano geometral. La recta r que pasa por C, es una recta frontal, y cortará a la recta AB en el punto 1. La paralela a 1C trazada por A, nos determina la intersección del plano con la cara frontal que contiene al punto A. Esta va unida con el punto C en la planta del poliedro. La paralela por B a la recta 1C, nos determina la intersección del plano con la cara frontal posterior, y donde corte con la arista lateral iría unida a C.

    El punto 2 es el resultado de la intersección de la prolongación de la recta frontal que pasa por A y la prolongación de la arista superior que iría unida con B en la cara superior y así podríamos acabar con la intersección.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. B4

    Nos dan el dibujo isométrico (sin coeficiente de reducción) de una pieza. Hay que dibujar la planta y el alzado (las vistas que consideramos oportunas) con los cortes adecuados para poder acotarla para su correcta definición dimensional usando normas UNE e ISO.

    Hemos hecho un corte por el plano de simetría en el alzado, para visualizar el interior de la pieza y en planta un corte parcial para acotar el ancho de el corte pasante inferior.

    Para acotarla hemos empleado: simetrías, redondeos, diámetros y alturas.

    Pues con este post, ya tenemos cubierto el examen de la convocatoria ordinaria y coincidentes de Dibujo Técnico de la EvAU de la Comunidad de Madrid del año 2024.

Mi solución por pasos al examen de Ingeniería de Tecnologías Industriales UPV, convocatoria ordinaría del examen de axonométrico 2024

     Esta es la solución que propongo al examen de Expresión Gráfica, de la Universidad Politécnica de Valencia en el Grado de Ingeniería Industrial, con fecha 17 de Abril del año 2024. Este examen fue el primer parcial de la materia de Dibujo Técnico, en concreto la parte de Sistema Axonométrico.

    Nos daban:

• Un plano definido por el paralelogramo 4567
• Otro plano paralelo al eje Z  definido por su proyección horizontal 1'2'3'
• Una recta AD
• Los tres coeficientes de reducción correspondiente a cada eje (creemos que los coeficientes estaban cambiados, los del x por el y y viceversa),  y además el dibujo estaba sometido a una escala de reducción 1:2. 

    Se pide 

• Dibujar la proyección directa y la lateral horizontal del prisma de bases ABC y DEF de aristas paralelas. 
• Hallar la altura del punto más alto de la base DEF 
• E indicar qué aristas del prisma son paralelas a los planos laterales coordenados.

    La imagen de abajo representa el examen

    En la imágen aparece el cálculo de la primera base ABC, sabiendo que se encuentra en el plano 123.

    Dibujamos las aristas laterales que pasan por los vértices B y C. Determinamos la proyección horizontal del punto D, sabiendo que pertenece al plano 4567.

    
    Hallamos los puntos E y F. Si seguimos estrictamente el enunciado el punto F quedaría fuera del paralelogramo 4567, pensamos que están cambiadas las escalas axonométricas de los ejes x e y. Más abajo pongo dibujada cómo sería la solución con las escalas cambiadas.

    Solución marcada en rojo y las respuestas a la posición de las aristas respecto a los planos coordenados y la altura del punto más elevado.

    Cómo prometimos en dos imágenes anteriores, ahora comparto cómo sería la solución al mismo examen con las escalas en los ejes x e y cambiadas. Cuando las cambiamos los puntos E y F quedarían como muestra la imágen.

    De nuevo marcamos la nueva solución en rojo, con las escalas corregidas y las respuestas a la posición de las aristas respecto a los planos coordenados y la altura del punto más elevado.

  

    En breve colocaré una explicación al examen del sistema diédrico de la misma convocatoria.

EvAU Comunidad de Madrid mi solución examen ordinario Dibujo Técnico 2024

     Aquí comento brevemente cómo he solucionado el examen que se realizó en el año 2024 de Dibujo Técnico II en la Comunidad de Madrid en la convocatoria ordinaria para el acceso de los alumnos a las Universidades españolas, es decir, la antigua Selectividad o PAU y la actual EvAU.

    Vamos a distribuirlas por bloque y opciones:

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. A1

    Nos piden determinar el eje radical de los circunferencias interiores. Los datos son las circunferencias c1 y c2.

    Hemos aplicado el procedimiento de la obtención del eje radical a partir de una circunferencia auxiliar. En este caso, no hemos optado por las tangentes debido a que no se pueden dibujar las rectas tangentes a dos circunferencias interiores.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN

• SISTEMA DIÉDRICO. A2

    Nos piden representar las proyecciones verticales de dos rectas r y s sabiendo que son perpendiculares entre sí y sabiendo las proyecciones horizontales de estas rectas.

    Abatiendo el plano que contiene ambas rectas, podemos dibujarlas perpendiculares usando un arco capaz de 90º que pasará por las trazas horizontales de las rectas y por el punto P abatido. Este proceso está dibujado en color azul y magenta.

    También se podía usar un atajo, dibujado en la imagen en color naranja. El atajo consistía en dibujar un arco capaz de 90º. Por que como una de las rectas es frontal, la recta r, la otra la proyección vertical de la recta s se ve perpendicular a la proyección vertical r. Esta perpendicularidad viene explicada por el teorema de las tres perpendiculares.

• PERSPECTIVA CABALLERA Y VISTAS. A3

    Dadas dos vistas de una pieza: el alzado y la planta; nos piden: dibujar el perfil derecho y la perspectiva caballera. Los ejes de dicho sistema axonométrico están dibujados y el coeficiente de reducción en el eje y de 3/4.

    Hallamos el perfil usando la correspondencia entre vistas y procedemos a dibujar su perspectiva caballera aplicando el coeficiente de reducción en el eje y. Para los ejes x y z llevamos las medidas tal cual.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. A4

    Nos dan la semivista de una pieza de revolución cortada a un cuarto. Tenemos que hallar la semivista que falta. Como esta parte de la pieza no está afectada por el corte, dibujaremos la parte externa.

    Para acotar la pieza hemos empleado las normas UNE. 

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. B1

   Nos piden calcular los ejes, vértices y focos de una elipse, partiendo de un foco, dos tangentes y la distancia focal, 2c.

   Hemos aplicado los conceptos métricos de la curva cónica, como: la simetría que producen las tangentes, a qué distancia se encuentran los focos y por donde pasa la circunferencia focal del otro foco.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN

• SISTEMA ISOMÉTRICO Y VISTAS. B2

     Dadas las tres vistas de una pieza: planta, alzado y perfil izquierdo, se pide hallar en planta el corte que produce el plano H y la representación isométrica de la pieza con el corte.

    Como nos indican en el enunciado que es dibujo isométrico, no tenemos que aplicar el coeficiente de reducción que es 0'816:1. Consecuencia: Las medidas se pueden coger tal cual de las vistas.

• PLANOS ACOTADOS. B3

     Nos dan la planta incompleta de una cubierta cuyos aleros están a la misma altura. Tenemos que dibujar los faldones sabiendo que se todos tienen la misma pendiente.

    Para las esquinas hemos dibujado las bisectrices.Para los faldones cuyas trazas son paralelas, hemos calculado la mediatriz de la distancia entre ambos. Y para los planos que sus trazas están en perpendicular, las hemos alargado y hallado sus bisectrices.  

    Uniendo convenientemente estas bisectrices y mediatrices, podremos completar la planta del tejado.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. B4

    Dada la perspectiva caballera de una pieza, tenemos que hallar la planta y el alzado de la misma para luego después proceder a su acotación.

    Como datos de la perspectiva, nos indican que el coeficiente de reducción del eje y es 1/2, por lo tanto, las medidas que estén ligadas a este eje las tendremos que dibujar al doble.

    En esta pieza el alzado presenta cierta simetría que se ha aprovechado para hacer una acotación por simetría. Las demás alturas y profundidades tiene una acotación poco reseñable.

    Esto es todo de momento,

    Saludos

Mi solución por pasos al examen de Ingeniería de Tecnologías Industriales UPV, convocatoria ordinaría del examen de axonométrico 2023

       El año pasado ayudé a un alumno a superar la asignatura de primer grado de Expresión gráfica de la Universidad Politécnica de Valencia. En mi post, no aporto casi nada nuevo a la solución propuesta por el profesor de dicha asignatura. Lo que quiero compartir es el proceso a seguir para poder solucionar este examen con éxito, y siempre respetando y valorando el trabajo de este profesor. 

    Primero comparto la imagen de este enunciado. Se propone una axonometría trimétrica con distintos coeficientes de reducción para cada eje coordenado: para el eje x 0'65, para el eje y 0'92 y para el eje z 0'86. Se pide a la escala natural dibujar un prisma por medio de rectas horizontales y apoyado en las chapas 1234 y 5678.

    Iniciamos el ejercicio dibujando la chapa 5678, en color azul. El plano se la contiene, es el plano proyectante formado por las rectas U y V.

    Después, dibujamos la perspectiva directa delas rectas R, S y T, dadas sus alturas y proyecciones sobre el plano coordenado XOY o plano Horizontal. En estas alturas, medida que corresponde al eje Z, hay que aplicarles el correspondiente coeficiente de reducción. Al realizar dicha operación, hemos aprovechado para poder hallar la verdadera magnitud de las distancias de los puntos 2-3 y 4-1, ambas con la misma distancia y paralelas al eje Z (apartado 6 del enunciado).

    La primera base del prisma es la intersección de estas rectas horizontales con la chapa vertical 1234, los puntos ABC.

    La segunda base del prisma que es la intersección de la chapa 5678 con las rectas horizontales, los puntos DEF.

    Por último, nos piden la sección plana que produce el plano vertical formado por la rectas M y N.

    Resalto la solución, el prisma y la sección plana del mismo.

    Espero que haya sido de ayuda este post, en breve haré lo mismo con el examen de diédrico. Para descargar estos pasos en pdf están en este enlace.