Mis soluciones al examen de Dibujo Técnico II de la Junta de Andalucía, convocatoria extraordinaria titular del año 2024

     Comparto mis soluciones al examen de Dibujo Técnico II del distrito único de la Junta de Andalucía. En concreto, convocatoria extraordinaria titular realizado en  Julio del año 2024.

    Aquí comento esos problemas y ejercicios del examen de Dibujo Técnico.

PROBLEMA 1: SISTEMA DIÉDRICO

En el problema del sistema diédrico nos dan la traza horizontal del plano P y las proyecciones horizontales de dos puntos, A y B. Con estos datos, tenemos que hallar un cubo o hexaedro apoyado en el plano P y el valor de su diagonal.

Nos dicen que A y B vértices de la base del cubo que está contenida en P. También dicen que los otros vértices de la misma base, C y D, están sobre el plano horizontal de proyección. Vemos que A y B se encuentran sobre una recta horizontal del plano, los que nos permite deducir que las aristas AD y BC están sobre rectas de máxima pendiente del plano y la verdadera magnitud de la arista del cubo. He partido de la base del cubo abatida, que es un cuadrado, para poder hallar la traza vertical del plano y la proyección de la misma, ABCD.

Para poder dibujar el resto del cubo, he trazado las rectas perpendiculares al plano que pasan por los vértices ABCD. Después he girado una de ellas, en concreto la que pasa por el punto B, hasta ponerla en posición frontal para poder colocar la magnitud de la arista donde se encuentra el punto F. Para finalizar el dibujo del cubo, he llevado paralelas a la base por F.

También he usado un giro para hallar la magnitud de la diagonal del cubo. La diagonal que he usado ha sido la HB.

PROBLEMA 2: SISTEMA AXONOMÉTRICO

En este problema tenemos representadas las vistas: planta, alzado y perfil, de una pieza a escala 3:5. Tenemos que dibujar la perspectiva isométrica de la pieza. 

Cuando nos ponernos a dibujar la pieza en isométrico, hay que pasarla a escala natural y aplicarle el coeficiente de reducción. Las perspectivas de  las circunferencias serán elipses. Estas elipses se dibujarán por cualquier procedimiento conocido: por afinidad, por el método de los 8 puntos...

Por último, debemos calcular la medida C. Recordar que para hallarla sólo aplicaremos la escala 3:5.

EJERCICIO 1: TRAZADOS GEOMÉTRICOS

Este ejercicio es un ejercicio sobre parábolas. Tenemos que dibujar una parábola sabiendo el foco, el eje y una recta tangente. Por otro lado tenemos que señalar: la directriz, el foco y el punto de tangencia con la recta dada.

He hallado la directriz por que sé que será perpendicular al eje y pasará por el simétrico de F respecto a la tangente. El vértice de la curva estará en el eje, a la mitad de la distancia del foco y la directriz. Trazando la perpendicular a la directriz por el simétrico de F, FS, hasta cortar a la tangente T, estará el punto de tangencia P.

La curva está dibujada por puntos.

EJERCICIO 2: TRANSFORMACIONES GEOMÉTRICAS

Después de definir una homología afín por el eje y dos puntos homólogos O y O', centros de la circunferencia y elipses afines, hay que representar la figura resultante de esta afinidad. Nos piden determinar los ejes de la elipse homóloga de la circunferencia.

A través de la construcción que transforma dos diámetros de la circunferencia en los ejes de la elipse, dibujaremos dicha elipse. 

Relacionando puntos y rectas de la estrella de la figura dada, vamos hallando lo que falta para determinar la figura afín: una estrella inscrita en una elipse. 

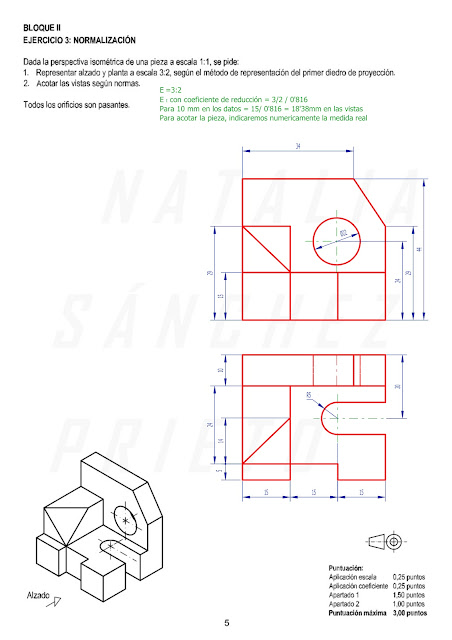
EJERCICIO 3: NORMALIZACIÓN

Partimos de la perspectiva isométrica de una pieza a escala 5:8, para dibujar su planta y alzado a escala 1:2. Para terminar el dibujo, nos piden que la acotemos las vistas según las normas ISO y UNE.

A estas vistas se le aplica el coeficiente de reducción (0'816/1) y aplicando la escala intermedia que hace pasar de la escala inicial (5:8) a la final (1:2), dibujo las vistas. Esta escala es la escala 4:5.

Después hemos acotado la pieza usando las medidas reales. Bien se puede aplicar la escala final tomándolas de las vistas que ya tenemos dibujadas o la inicial después de quitarle el coeficiente de reducción.

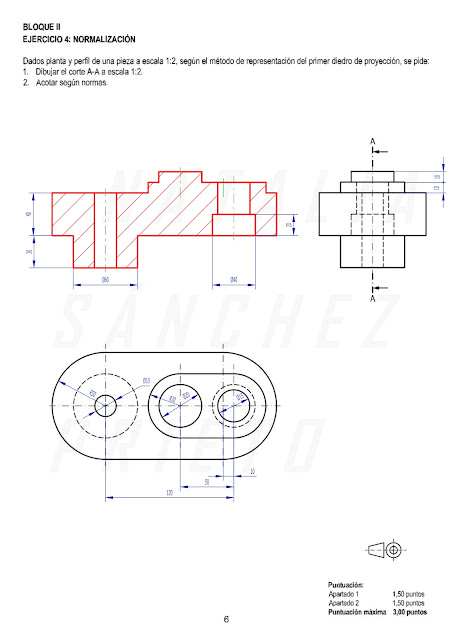
EJERCICIO 4: NORMALIZACIÓN

En este ejercicio tenemos que hacer un corte total en el perfil izquierdo partiendo de la planta y el alzado de la pieza dada a escala 1:2. 

El plano de corte pasará por el eje del cilindro más alto y será de perfil. Procedemos a relacionar las vistas para resolver el corte.

Dibujamos el corte y acotamos la pieza con las medidas reales aplicando la escala 1:2.

Esto es todo. ¡¡¡Ánimo a los estudiantes!!!

Mis soluciones al examen de Dibujo Técnico II de la Junta de Andalucía, convocatoria ordinaria suplente del año 2024

    Comento mis soluciones a los ejercicios del examen de Dibujo Técnico II de la convocatoria ordinaria suplente de este año 2024. Estos enunciados están publicados en la página web de la Universidad de Andalucía en la sección de exámenes de PEvAU o antigua selectividad.

    Procedo a distribuirlos por los bloques I y II y sus correspondientes apartados (problemas y ejercicios)

BLOQUE I

PROBLEMA 1: SISTEMA DIÉDRICO

    Nos dan las proyecciones de dos puntos y tenemos que pasar por ellos un plano que forma 45º con el plano horizontal de proyección. De todas las opciones que podemos dibujar, nos piden que dibujemos las trazas que formen un ángulo agudo en el primer diedro o cuadrante. En la imagen es el plano P en color verde.

    Los puntos dato, A y B, son los vértices consecutivos de un tetraedro que tenemos que dibujar apoyado sobre el plano P. He abatido el plano para colocar la base y he aprovechado en el abatimiento para poder calcular la altura de dicho poliedro regular. Colores magenta y azul.

    Por último, he indicado las partes vistas y ocultas del sólido y la altura numérica del poliedro, como se perdía en el enunciado.

PROBLEMA 2: SISTEMA AXONOMÉTRICO

    Dadas las vistas de un sólido: planta, alzado y perfil derecho a escala 2:3; nos piden dibujar la perspectiva isométrica de la pieza a escala natural 1:1. También quieren que indiquemos la medida real de la magnitud "C".

    Como las vistas están a una escala y tenemos que incluir el coeficiente de reducción, he indicado los pasos numéricos que tenemos que seguir para poder realizar las operaciones con un solo cálculo. En color verde.

    El valor numérico de "C" se calcula aplicando la escala 2:3.

BLOQUE II

EJERCICIO 1: TRAZADOS GEOMÉTRICOS

    Nos dan dos circunferencias y el punto de tangencia en una de ellas. Nos piden el eje radical de las dos circunferencias dadas y las circunferencias tangentes a ambas, cuyo punto de tangencia sea T.

    He hallado el eje radical de ambas circunferencias, en color verde. Y he aplicado los procedimientos de Apolonio para resolver este caso que es un caso especial de CCT (circunferencia, circunferencia, punto).

EJERCICIO 2: TRANSFORMACIONES GEOMÉTRICAS

    Nos encontramos una homología afín determinada por tres puntos afines, A-A', O-O' y N-N', este último es un punto doble. Nos piden que hallemos la figura afín a la dada (parece un lapicero) y dibujar el eje de la afinidad, así como, los semiejes de la elipse. 

    He hallado los semiejes de la mitad de la elipse en la que se transforma la mitad de la circunferencia que se nos representa como una goma del lápiz.  En color magenta.

    El resto de la figura se resuelve como una afinidad normal. He aprovechado el paralelismo entre las rectas y el paralelismo que tienen algunos segmentos con el eje. Recordar que la afinidad mantiene el paralelismo entre rectas.

EJERCICIO 3: NORMALIZACIÓN

    Tenemos dibujado una perspectiva isométrica a escala natural 1:1, y nos piden dibujar la planta y el alzado a escala 3:2 para luego acotarla según normas.

    Las operaciones oportunas que tenemos que realizar con las escalas las he puesto en color verde. 

    La acotación obedece a las medidas reales, las he calculado a partir de las vistas y aplicando la escala.

EJERCICIO 4: NORMALIZACIÓN

    Tenemos que realizar el corte A-A en alzado de la pieza dada por su planta y perfil izquierdo. Las vistas están dibujadas a escala 1:2.

    He realizado el corte y acotado poniendo las medias reales que se deducen de aplicar la escala 1:2. Lo más reseñable de esta pieza, a mi parecer, es la colocación de las circunferencias y su acotación.

    Estos son mis comentarios a mis soluciones al examen suplente de Dibujo Técnico II de la PEvAU de Andalucía del año 2024.

EvAU Comunidad de Madrid mi solución examen extraordinario coincidentes Dibujo Técnico 2024

     Vamos por el último post de la EvAU (antigua selectividad y PAU) de la Comunidad de Madrid del examen de Dibujo Técnico II del año 2024 de la convocatoria extraordinaria y coincidentes (de los exámenes de las asignaturas específicas) de Julio. Quiero recordar que la intención de mis post es intentar ser aclaratorios, complementarios a cualquier publicación haya realizado cualquier universidad madrileña con las soluciones a dicho examen. 

    Procedo a distribuir los problemas planteados por opciones, bloques y ejercicios

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO A1.

    En el ejercicio aparecían dibujados dos rectas y un punto. Nos pedía determinar las circunferencias tangentes a las rectas y que a su vez pasaran por el punto dado A.

    Lo he resuelto por potencia, como nos indica Apolonio en el caso de punto recta recta (rrP). 

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO A2

    Nos dan tres rectas: h, s y r. Nos piden dibujar la recta paralela a h que se apoya o corta a r y s. 

    Lo he resuelto por cambio de plano. He dibujado dos planos paralelos a h que contuvieran a r y a s. Después, he hallado la intersección de ambos planos. La recta intersección de estos planos es la solución pedida, la recta m.

    Otra manera de resolverlo hubiera sido hallando un plano paralelo a h que pasara por una de las rectas, r o s. Y después, hallar la intersección de este plano con la otra recta. Por último, trazamos la paralela a h por ese punto de intersección.

    Viene comprobado en color magenta que la recta m efectivamente corta a r y s en un punto.

• SISTEMA AXONOMÉTRICO. EJERCICIO A3.

    Venían dibujadas la planta y el alzado de una pieza. Nos pedían que representar la pieza el dibujo isométrico (sin coeficiente de reducción). Las circunferencias isométricas las debíamos dibujar cómo óvalo isométrico y no como elipses. También teníamos que indicar los centros de las circunferencias que definen dichos óvalos.

    He dibujado las partes útiles del cuadrado que circunscribe la circunferencia para poder indicar y calcular dichos los centros.

    Después, los he desplazado siguiendo el eje z y el eje y, para obtener el grosor de la figura.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO A4

    Tenemos una pieza representada en dibujo isométrico (sin coeficiente de reducción) y nos piden que realicemos las vistas necesarias con las secciones que consideremos oportunas para poder definir la pieza. También pedían acotar las vistas para su definición dimensional siguiendo las normas ISO y UNE.

    El alzado y la planta son vistas suficientes para poder apreciar el volumen de la pieza. Y para poder acotar la parte interna izquierda, la cota 10, he optado por un corte parcial.

    En la acotación, donde más variaciones de cotas podemos encontrar es en la parte derecha de la pieza. Hemos indicado las totalidades y los radios.

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO B1.

    Nos dan dos puntos de una parábola y su foco. Teníamos que hallar la directriz, el eje y las tangentes por esos puntos a la parábola.

    Hemos dibujado las circunferencias que pasan por F y tienen sus centros en A y B. La directriz será la tangente exterior a dichas circunferencias, he escogido la tangente superior. Perpendicular a la directriz por el foco se encuentra el eje.

    Para trazar las tangentes, hemos dibujado los radios vectores, y perpendicular a la línea que une los extremos, estarán las tangentes.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO B2

    Tenemos que hallar la sección que produce el plano ABCD en el paralepípedo o ortoedro. 

    Como el plano ABCD es un plano paralelo a la línea de tierra, he resuelto la sección en tercera proyección. 

    También he incluido los lados vistos y ocultos de la figura plana sección.

• PERSPECTIVA CÓNICA. EJERCICIO B3

    Sobre un poliedro en perspectiva cónica, debemos dibujar la pieza que viene dada por sus tres vistas: planta, alzado y perfil.

    El misterio de este ejercicio se encontraba en hallar el punto medio del alzado. Para poder hallarlo, he obtenido el punto de fuga de las aristas paralelas y dibujado las diagonales de la planta. En color verde. 

    Para concretar la pieza he unido convenientemente los puntos obtenidos en las aristas del sólido.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO B4

    Tenemos en dibujo isométrico (sin coeficiente de reducción), una pieza cuyo plano de simetría horizontal era coincidente con el plano xoy. Había que dibujar las vistas necesarias para poder acotar la pieza con los cortes necesarios para su correcta definición. Hay que tener en cuenta las normas industriales ISO y UNE para su ejecución.

    En el alzado le hemos aplicado un corte al cuarto. En las medidas hemos tenido el cuenta el plano de simetría que definen el eje y. 

    Esta es mi propuesta a la solución al examen de EvAU de la convocatoria extraordinaria coincidentes del año 2024 de la Comunidad de Madrid de Dibujo Técnico II.

EvAU Comunidad de Madrid mi solución examen extraordinario Dibujo Técnico 2024

     Voy a exponer mi propuesta a las soluciones al examen de Dibujo Técnico II de la EvAU (antigua selectividad o PAU) de la Comunidad de Madrid de la convocatoria extraordinaria que se celebró en Julio de 2024. Recordar que la Universidad Complutense de Madrid (supongo que otras Universidades madrileñas también las compartirán) comparte las soluciones, y yo trato de aportar, cuando se pueda, una alternativa o un complemento a estas soluciones.

    Procedo a distribuir el examen por bloques y ejercicios.

OPCIÓN A

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO A1.

    Nos dan una figura, ABCD, formada por un arco y tres rectas. Tenemos que transformarla en una figura inversa. Los datos de la inversión son el centro y un punto doble.

    Tenemos los dos casos importantes de la transformación de una recta: la que pasa por O que se transforma en sí misma, y la que no pasa por O que se transforma en una circunferencia que si pasa por O. Sabemos que O es el centro de inversión y que E un punto doble. Dibujamos la circunferencia de puntos dobles y con ella podemos calculamos los inversos de A y D que son A' y D', respectivamente. Después, aplicamos los casos indicados al inicio del párrafo.

    Con los arcos que pasan por A' y D' hallamos B' y C', y con ello la recta inversa que resulta de transformar el arco de BC.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. EJERCICIO A2

    Nos dan una semiesfera y la proyección horizontal de un punto A. Nos dicen que A es el punto perteneciente a la semiesfera y que por A pasa una recta frontal que atraviesa el sólido. El punto B, es el punto de salida de la recta frontal y además se encuentra situado a una distancia d de A.
    Para resolverlo, he pasado un plano frontal por el punto A. He hallado la sección de ese plano frontal con la semiesfera para poder calcular la posición de los puntos A y B.
    Por último, he diferenciado las partes vistas de las ocultas de la recta.

• PERSPECTIVA CÓNICA. EJERCICIO A3

    En este ejercicio, proponen que dibujemos la sección que produce un plano que pasa por tres puntos A, B y C en un poliedro. 
    Como es una perspectiva cónica frontal, sabemos que las rectas paralelas al plano geometral se van a seguir viendo paralelas en cualquier otra altura o posición. He consderado el sólido como si fuera un paralepípedo. El segmento AB se encuentra en la cara superior, paralela al suelo, por lo tanto, si cortamos el sólido por un plano horizontal que pasa por C, la sección que produce será un paralelogramo igual que sus bases, en color azul claro. Al trazar la paralela por C a AB donde corte, en este caso, con la arista opuesta, tendremos un punto de la sección.
    La sección azul clara es la que se produciría si el sólido fuera un paralepípedo. Para dibujar la solución tomaremos los puntos en común las aristas del poliedro con la sección azul, en color rojo. 

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO A4
    Dada la perspectiva isométrica de una pieza, nos piden representar las tres vistas: planta, alzado y perfil derecho.
    Al ser un dibujo isométrico no tenemos que tener en cuenta el coeficiente de reducción (0'816:1), tomaremos las medidas directamente, siempre que estén sobre aristas paralelas a los ejes coordenados.

OPCIÓN B

BLOQUE 1: GEOMETRÍA PLANA Y DIBUJO TÉCNICO. EJERCICIO B1.

    En este ejercicio nos dan una figura ABCDE y tenemos que hallar su figura afín A'B'C'D'E'. Para definir la homología afín, aparecen dibujados el eje y dos puntos afines, A y A'.

    He empezado a dibujar la recta AB, por pasar por A y ser paralela al eje. Las rectas paralelas al eje sus afines también serán paralelas entre sí, por ser su punto doble impropio. Después he hallado B' trazando paralela a la dirección de afinidad.

    Lo siguiente que podemos hacer es hallar las afines de las rectas AE o BC, usando el corte del las prolongación de las mismas con el eje, es decir, su punto doble. De esta manera podemos ir acabando la figura afín.

BLOQUE 2: SISTEMAS DE REPRESENTACIÓN 

• SISTEMA DIÉDRICO. B2

    Como datos tenemos dibujados dos rectas h y r y un punto P. Nos piden que dibujemos una recta perpendicular a ambas y que pase por P.
    Mi proceder ha sido: hallar el plano que contiene a P y es paralelo a  h y r  y después trazar la recta perpendicular a dicho plano. Para hallar la dirección de la recta perpendicular al plano, he usado las rectas frontales y horizontales de dicho plano.

• PLANOS ACOTADOS. EJERCICIO B3

    Nos dan el contorno exterior de una cubierta, cuyas vertientes tienen una inclinación de 30º con el plano horizontal de proyección. Al no indicar nada en el enunciado, entendemos que los faldones se encuentra a la misma altura. Nos piden dibujar la parte que falta del tejado.
    Al tener todos los faldones la misma inclinación, he trazado la bisectriz para aquellos que sus trazas forman un ángulo, en este caso de 90º. Para los tejados cuyas trazas son paralelas, hemos trazado la mediatriz. 
    Para la zona interior, hemos prolongado las trazas hasta que se corten y hemos trazado su bisectriz.
    Marcando convenientemente estas líneas, obtenemos las aristas de intersección que produce estos planos de 30º, es decir, las limatesas, limahoyas y caballetes.

BLOQUE 3: DOCUMENTACIÓN GRÁFICA Y PROYECTOS. EJERCICIO B4

    Partimos de la planta y la mitad del alzado cortado a un cuarto, en concreto la parte afectada por el corte (la parte interna). Nos piden: hallar la parte externa del alzado que falta y acotarlo.
    He dibujado la parte externa que falta del alzado y acotado la pieza. Destacar que la planta se ha usado la acotación por simetría y en el alzado se han indicado los radios de la parte superior, son así por ser arcos de 180º. 

    Esta es mi propuesta de solución al examen de Dibujo Técnico II de la EvAU de la Comunidad de Madrid en su convocatoria extraordinaria del año 2024.